3D 碰撞检测 - 游戏开发

轴对齐包围盒

与 2D 碰撞检测一样，**轴对齐包围盒** (AABB) 是确定两个游戏实体是否重叠的最快算法。它包括将游戏实体包裹在一个不旋转（因此轴对齐）的盒子中，并检查这些盒子在 3D 坐标空间中的位置，以查看它们是否重叠。

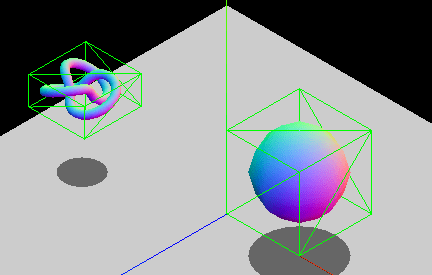
Two 3-D non-square objects floating in space encompassed by virtual rectangular boxes.

出于性能原因，存在**轴对齐约束**。两个不旋转盒子之间的重叠区域可以通过纯逻辑比较来检查，而旋转盒子则需要额外的三角函数运算，计算速度较慢。如果您的实体会旋转，您可以修改包围盒的尺寸，使其仍然包裹对象，或者选择使用其他包围几何体类型，例如球体（它们不受旋转影响）。下面的动画 GIF 展示了一个 AABB 动态调整大小以适应旋转实体的图形示例。该盒子不断改变尺寸以紧密贴合内部的实体。

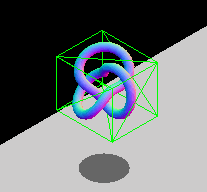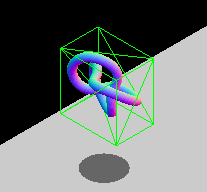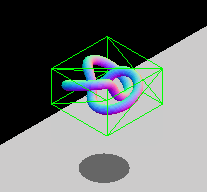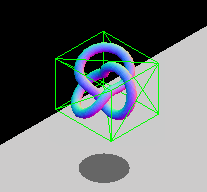
Animated rotating knot showing the virtual rectangular box shrink and grow as the knots rotates within it. The box does not rotate.

注意： 请参阅使用 Three.js 进行包围体碰撞检测文章，了解此技术的实际实现。

点 vs. AABB

检查一个点是否在 AABB 内非常简单——我们只需检查点的坐标是否落在 AABB 内；分别考虑每个轴。如果我们假设 P_x、P_y 和 P_z 是点的坐标，而 B_minX–B_maxX、B_minY–B_maxY 和 B_minZ–B_maxZ 是 AABB 每个轴的范围，我们可以使用以下公式计算两者之间是否发生了碰撞：

f(P, B)= (P_x \ge B_{minX} \wedge P_x \le B_{maxX}) \wedge (P_y \ge B_{minY} \wedge P_y \le B_{maxY}) \wedge (P_z \ge B_{minZ} \wedge P_z \le B_{maxZ})

或者在 JavaScript 中：

function isPointInsideAABB(point, box) {
  return (
    point.x >= box.minX &&
    point.x <= box.maxX &&
    point.y >= box.minY &&
    point.y <= box.maxY &&
    point.z >= box.minZ &&
    point.z <= box.maxZ
  );
}

AABB vs. AABB

检查一个 AABB 是否与另一个 AABB 相交与点测试类似。我们只需要对每个轴进行一次测试，使用盒子的边界。下图展示了我们在 X 轴上执行的测试——基本上，范围 A_minX–A_maxX 和 B_minX–B_maxX 是否重叠？

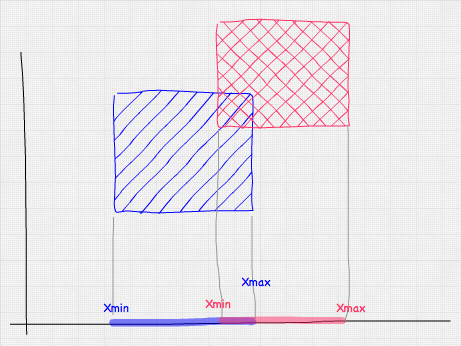
Hand drawing of two rectangles showing the upper right corner of A overlapping the bottom left corner of B, as A's largest x coordinate is greater than B's smallest x coordinate.

从数学上讲，这看起来是这样的：

f(A, B) = (A_{minX} \le B_{maxX} \wedge A_{maxX} \ge B_{minX}) \wedge ( A_{minY} \le B_{maxY} \wedge A_{maxY} \ge B_{minY}) \wedge (A_{minZ} \le B_{maxZ} \wedge A_{maxZ} \ge B_{minZ})

在 JavaScript 中，我们会这样做：

function intersect(a, b) {
  return (
    a.minX <= b.maxX &&
    a.maxX >= b.minX &&
    a.minY <= b.maxY &&
    a.maxY >= b.minY &&
    a.minZ <= b.maxZ &&
    a.maxZ >= b.minZ
  );
}

包围球

使用包围球进行碰撞检测比 AABB 稍微复杂一些，但仍然相当快速。球体的优点在于它们不受旋转影响，因此如果被包裹的实体旋转，包围球仍然是相同的。它们的主要缺点是，除非它们包裹的实体实际上是球形的，否则包裹通常不合适（例如，用包围球包裹一个人会产生大量误报，而 AABB 会是更好的匹配）。

点 vs. 球

要检查一个球体是否包含一个点，我们需要计算点与球体中心之间的距离。如果该距离小于或等于球体的半径，则该点在球体内部。

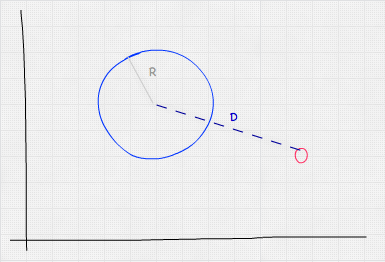
Hand drawing of a 2D projection of a sphere and a point in a Cartesian coordinate system. The point is outside of the circle, to the lower right of it. The distance is denoted by a dashed line, labeled D, from the circle's center to the point. A lighter line shows the radius, labeled R, going from the center of the circle to the border of the circle.

考虑到两点 A 和 B 之间的欧几里得距离为： $\sqrt{(A_x - B_x)^2 + (A_y - B_y)^2 + (A_z - B_z)^2}$ ，我们的点与球体碰撞检测公式将如下所示：

f(P,S) = S_{radius} \ge \sqrt{(P_x - S_x)^2 + (P_y - S_y)^2 + (P_z - S_z)^2}

或者在 JavaScript 中：

function isPointInsideSphere(point, sphere) {
  // we are using multiplications because is faster than calling Math.pow
  const distance = Math.sqrt(
    (point.x - sphere.x) * (point.x - sphere.x) +
      (point.y - sphere.y) * (point.y - sphere.y) +
      (point.z - sphere.z) * (point.z - sphere.z),
  );
  return distance < sphere.radius;
}

注意： 上面的代码包含一个平方根，计算成本可能很高。一个简单的优化方法是比较平方距离与平方半径，因此优化后的方程将涉及 distanceSqr < sphere.radius * sphere.radius。

球 vs. 球

球体与球体测试与点与球体测试类似。我们需要测试的是球体中心之间的距离是否小于或等于它们半径之和。

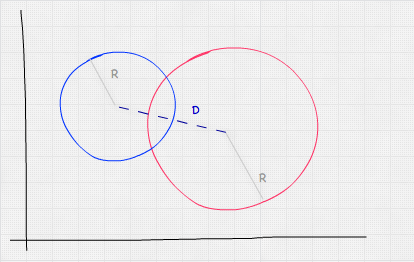
Hand drawing of two partially overlapping circles. Each circle (of different sizes) has a light radius line going from its center to its border, labeled R. The distance is denoted by a dotted line, labeled D, connecting the center points of both circles.

从数学上讲，这看起来像：

f(A,B) = \sqrt{(A_x - B_x)^2 + (A_y - B_y)^2 + (A_z - B_z)^2} \le A_{radius} + B_{radius}

或者在 JavaScript 中：

function intersect(sphere, other) {
  // we are using multiplications because it's faster than calling Math.pow
  const distance = Math.sqrt(
    (sphere.x - other.x) * (sphere.x - other.x) +
      (sphere.y - other.y) * (sphere.y - other.y) +
      (sphere.z - other.z) * (sphere.z - other.z),
  );
  return distance < sphere.radius + other.radius;
}

球 vs. AABB

测试球体和 AABB 是否碰撞稍微复杂一些，但仍然简单快捷。一个合乎逻辑的方法是检查 AABB 的每个顶点，并对每个顶点进行点与球体测试。然而，这有点大材小用——测试所有顶点是不必要的，因为我们只需要计算 AABB 的最近点（不一定是顶点）与球体中心之间的距离，看看它是否小于或等于球体的半径。我们可以通过将球体的中心限制到 AABB 的范围内来获得这个值。

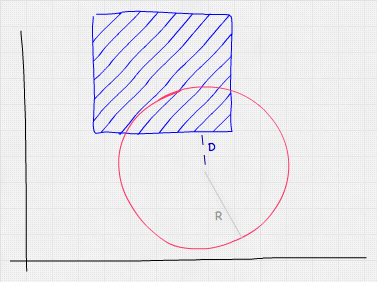
Hand drawing of a square partially overlapping the top of a circle. The radius is denoted by a light line labeled R. The distance line goes from the circle's center to the closest point of the square.

在 JavaScript 中，我们会这样进行测试：

function intersect(sphere, box) {
  // get box closest point to sphere center by clamping
  const x = Math.max(box.minX, Math.min(sphere.x, box.maxX));
  const y = Math.max(box.minY, Math.min(sphere.y, box.maxY));
  const z = Math.max(box.minZ, Math.min(sphere.z, box.maxZ));

  // this is the same as isPointInsideSphere
  const distance = Math.sqrt(
    (x - sphere.x) * (x - sphere.x) +
      (y - sphere.y) * (y - sphere.y) +
      (z - sphere.z) * (z - sphere.z),
  );

  return distance < sphere.radius;
}

使用物理引擎

3D 物理引擎提供了碰撞检测算法，其中大多数也基于包围体。物理引擎的工作方式是创建一个物理体，通常附加到其视觉表示上。该身体具有速度、位置、旋转、扭矩等属性，以及一个物理形状。这个形状是碰撞检测计算中考虑的因素。

我们准备了一个实时碰撞检测演示（附带源代码），您可以查看以了解这些技术的实际应用——它使用了开源的 3D 物理引擎 cannon.js。

另见

MDN 上的相关文章

外部资源

帮助改进 MDN

了解如何贡献

此页面最后修改于 2025 年 7 月 11 日，由 MDN 贡献者编辑。

在 GitHub 上查看此页面 • 报告此内容的问题