视点和观察者：在 WebXR 中模拟相机

摄像机与相对运动

当拍摄一部经典的真人电影时，演员在布景上表演，随着他们的表演在布景中移动，有一台或多台摄像机监视着他们的动作。摄像机可能固定在原地，但也可能设置成随之移动，跟踪表演者的动作，前后推拉以达到情感效果等等。

虚拟摄像机

在 WebGL (以及扩展到 WebXR) 中，没有我们可以移动和旋转的摄像机对象，所以我们必须找到一种方法来伪造这些运动。既然没有摄像机，我们必须找到一种方法来模拟它。幸运的是，像伽利略、牛顿、洛伦兹和爱因斯坦这样的物理学家给了我们相对性原理，该原理指出物理定律在所有参考系中具有相同的形式。也就是说，无论你站在哪里，物理定律都以相同的方式运作。

推而广之，如果你和另一个人站在一个空旷的、一望无际的坚实石地上，如果你向另一个人移动三米，结果看起来就像另一个人向你移动了三米一样。你们俩都无法看出区别。第三方可以看出区别，但你们俩不能。如果你是一台摄像机，你可以通过移动摄像机或移动摄像机周围的一切来获得相同的视觉效果。

这就是我们的解决方案。由于我们无法移动摄像机，我们移动它周围的世界。我们的渲染器需要知道我们想象中的摄像机位置，然后改变每个可见对象的位置以模拟该位置和方向。因此，在 WebGL 和 WebXR 编程中，摄像机一词不是指实际的摄像机对象，而是指描述场景中假设观看者的位置和观看方向的对象，无论 3D 空间中是否存在实际对象。

视角

由于摄像机是一个虚拟对象，它不一定代表虚拟世界中的物理对象，而是代表观看者的位置和观看方向，因此思考需要使用摄像机的情况很有用。与游戏相关的情况单独列出，因为它们通常是特定于游戏的特殊情况，但这些视角中的任何一个都可能适用于任何 3D 图形场景。

通用摄像机

一般来说，虚拟摄像机可能与场景中的物理对象结合，也可能不结合。事实上，在 3D 游戏范围之外，摄像机根本不对应场景中出现的对象的可能性要大得多。以下是 3D 摄像机的一些使用示例：

• 在渲染动画时——无论是用于电影制作还是用于演示或游戏——虚拟摄像机就像现实世界的电影摄像机一样使用。尽可能地使用标准电影摄影技术，因为观众很可能从小就看着使用这些技术的电影长大，并且潜意识里期望电影或动画会遵循这些方法。偏离这些方法可能会让观众出戏。
• 在商业应用中，3D 摄像机用于在渲染图表等内容时设置表观大小和透视。
• 在地图应用中，摄像机可以直接放置在场景上方，也可以使用各种角度来展示透视效果。对于 3D GPS 解决方案，摄像机的位置会显示用户周围的区域，显示屏的大部分区域显示用户移动路径前方的区域。
• 当使用 WebGL 加速 2D 图形绘制时，摄像机通常直接放置在场景中心上方，并设置距离和视野以允许显示整个场景。
• 在加速位图图形时，渲染器会将 2D 图像绘制到 WebGL 纹理的缓冲区中，然后重新绘制纹理以刷新屏幕。这实质上是使用纹理作为执行 2D 图形应用程序中的多重缓冲的后台缓冲区。

游戏中的摄像机

游戏种类繁多，因此，摄像机在游戏中的使用方式也有多种。一些常见情况包括：

• 在第一人称游戏中，摄像机位于玩家角色的头部内，面向与角色眼睛相同的方向。这样，玩家屏幕或头戴设备上呈现的视图就是他们角色所看到的。
• 在某些第三人称游戏中，摄像机位于玩家角色或载具后方不远处，显示他们在游戏世界中移动时的背影。这在许多多人在线角色扮演游戏、某些射击游戏等中都有使用。流行的例子包括《魔兽世界》、《古墓丽影》和《堡垒之夜》。此类别还包括摄像机放置在玩家肩上方的游戏。
• 一些 3D 游戏提供改变视点的能力，例如在飞行模拟器中查看飞机各个窗户的景色，或者查看游戏关卡中所有安全摄像头的视图（间谍和潜行类游戏中的常见功能）。此功能也用于提供带瞄准镜武器的游戏，此时视图不再完全基于头部位置。
• 3D 游戏还可能为非玩家提供观察动作的能力，可以通过放置一种隐形虚拟形象，或者选择一个固定的虚拟摄像机进行观察。
• 在高级 3D 游戏中，摄像机或类似摄像机的对象可以用来确定非玩家角色能看到什么，这依赖于玩家角色使用的相同渲染和物理引擎。
• 在单屏 2D 游戏中，摄像机不直接与玩家或游戏中的任何其他角色关联，而是固定在游戏区域上方或旁边，或者随着动作在滚动游戏世界中移动而跟随动作。例如，像《吃豆人》这样的经典街机游戏发生在一个固定的游戏地图上，因此摄像机保持固定在地图上方一定距离处，始终垂直向下指向游戏世界。
• 在像《超级马里奥兄弟》这样的横向卷轴或纵向卷轴游戏中，摄像机左右（或上下，或两者）移动，以确保即使游戏关卡比视口大得多，动作也始终可见。

定位摄像机

由于 WebGL 或 WebXR 中没有标准的摄像机对象，我们需要自己模拟摄像机。在此之前，以及我们模拟摄像机运动之前，让我们先来看看虚拟摄像机及其在最基本层面上如何移动。像所有事物一样，空间中对象（即使是虚拟空间）的位置可以使用三个数字来表示，这些数字表示其相对于原点（其位置定义为 (0, 0, 0)）的位置。

空间中物体与原点的空间关系还有一个方面需要考虑：透视。透视，如果正确应用于场景中的物体，可以将一个看起来像典型的 2D 屏幕一样平坦的场景，使其看起来像真实的 3D。透视有几种类型；这些类型及其数学解释在文章WebGL 模型视图投影中定义和解释。重要的是，透视对向量的影响可以通过向向量添加第四个分量来表示：透视分量，称为w。

w 的值通过将其他三个分量除以它来获得最终位置或向量；也就是说，对于给定为 (x, y, z, w) 的坐标，3D 空间中的点实际上是 (x/w, y/w, z/w, 1) 或 (x/w, y/w, z/w)。如果你不使用透视，w 总是 1。在这种情况下，位于 (1, 0, 3) 的对象的完整坐标是 (1, 0, 3, 1)。

但位置不足以描述 3D 空间中的对象，因为对象的空间状态不仅与其位置有关，还与其旋转或朝向方向（也称为其方向）有关。方向可以使用 3D 向量表示，该向量通常归一化，使其长度为 1.0。例如，如果对象面向位于 (3, 1, -2) 的对象——即向右三米，向上​​一米，距离原点两米——结果是

这也可以表示为数组

let directionVector = [3, 1, -2];

为了执行涉及坐标和朝向方向向量的操作，向量需要包含w分量。对于向量，w的值始终为0，因此上述向量也可以表示为[3, 1, -2, 0]或

WebXR 会自动将向量归一化为 1 米的长度；但是，你可能会发现出于各种原因自己进行归一化是有意义的，例如通过不必重复执行归一化来提高计算性能。

一旦你确定了表示你希望摄像机执行的组合运动的矩阵，你需要将其反转，因为你没有移动摄像机。由于你实际上正在移动除了摄像机之外的所有东西，所以取变换矩阵的逆矩阵以获得逆变换矩阵。然后可以将此逆矩阵应用于世界中的对象，以改变它们的位置和方向，从而模拟所需的摄像机位置。

这就是为什么 WebXR 用于表示变换的 XRRigidTransform 对象包含 inverse 属性的原因。inverse 属性是另一个 XRRigidTransform 对象，它是父变换的逆变换。由于表示视图的 XRView 具有一个 transform 属性，它是一个提供摄像机视图的 XRRigidTransform，你可以像这样获取模型视图矩阵——模拟所需摄像机位置所需的世界移动变换矩阵：

let viewMatrix = view.transform.inverse.matrix;

如果您使用的库直接接受 XRRigidTransform 对象，则可以直接获取 view.transform.inverse，而不是只提取表示视图矩阵的数组。

组合多个变换

如果你的摄像机需要同时执行多个变换，例如同时缩放和平移，你可以将变换矩阵相乘，将它们组合成一个单一的矩阵，一次性应用所有更改。请参阅文章Web 的矩阵数学中的两个矩阵相乘，了解执行此操作的清晰易读的函数，或者使用你喜欢的矩阵数学库（例如glMatrix）来完成工作。

重要的是要记住，与典型的算术不同，乘法是可交换的（也就是说，无论是从左到右还是从右到左相乘，结果都相同），矩阵乘法是不可交换的！这是因为每个变换都会影响对象的位置，甚至可能影响坐标系本身，这会极大地改变下一个操作的结果。因此，在构建复合变换（或直接按顺序应用变换）时，需要注意应用变换的顺序。

应用变换

要应用变换，你需要将点或向量乘以变换或变换组合。

这是对物理位置、方向或朝向方向以及透视概念的非常快速的概述。有关该主题的更多详细信息，请参阅文章几何和参考空间、WebGL 模型视图投影和Web 的矩阵数学。

模拟经典电影摄影

电影摄影是一门设计、规划和执行摄像机运动的艺术，旨在为动画或电影中的场景创造所需的视觉效果和情感。有许多术语有助于理解，主要围绕摄像机运动，因为这些术语用于描述虚拟摄像机设计的视点变化。同时执行多个这些运动也是完全可能的；例如，您可以在平移摄像机的同时放大场景。

请记住，大多数摄像机运动是相对于摄像机的参考空间来描述的。

矩阵的存储格式通常是列主序的平面数组；也就是说，矩阵的值从左上角开始，向下移动到底部，然后向右移动一行并重复，直到所有值都在数组中。

因此，一个看起来像这样的矩阵：

在数组形式中表示如下：

let matrixArray = [
  a1, a2, a3, a4,
  a5, a6, a7, a8,
  a9, a10, a11, a12,
  a13, a14, a15, a16,
];

在此数组中，最左边的列包含条目 a1、a2、a3 和 a4。最上面的行包含条目 a1、a5、a9 和 a13。

请记住，大多数 WebGL 和 WebXR 编程是使用第三方库完成的，这些库通过添加例程来扩展 WebGL 的基本功能，这些例程不仅更容易执行核心矩阵和其他操作，而且通常还更容易模拟这些标准电影摄影技术。您应该强烈考虑使用其中之一，而不是直接使用 WebGL。本指南直接使用 WebGL，因为它有助于在一定程度上了解其内部工作原理，并有助于库的开发或帮助您优化代码。

缩放

最著名的摄像机效果之一是变焦。变焦是在物理摄像机中通过改变镜头的焦距来完成的；这是镜头中心本身与摄像机感光元件之间的距离。因此，变焦实际上根本不涉及移动摄像机。相反，变焦镜头会随着时间的推移改变摄像机的放大倍数，使焦点区域看起来离观看者更近或更远，而无需实际物理移动摄像机。缓慢的移动可以给场景带来运动感、轻松感或焦点感，而快速的变焦可以制造焦虑、惊喜或紧张感。

由于变焦不移动摄像机位置，因此产生的效果是不自然的。人眼没有变焦镜头。我们通过远离或靠近物体来使它们变小或变大。在电影摄影中，这被称为推拉镜头。

3D 图形中有两种技术可以创建相似但不相同的结果，并且它们的方法在不同情况下更容易应用。

通过调整视场进行缩放

您可以通过改变摄像机的视场 (FOV) 来实现更接近真实“缩放”的效果。视场是一个角度，定义了摄像机周围整个可见区域中应该同时可见的弧线长度。这是物理摄像机中焦距的一种效果，因此，由于没有真实的摄像机，改变 FOV 是一个可行的替代方案。

回想一下，圆的周长是 2π⋅r 弧度 (360°)；因此，这是理论上的最大 FOV。然而，实际上，人类不仅看不到那么多，而且显示器和 VR 眼镜等观看设备往往会进一步缩小视场。人眼通常具有约 135°（约 2.356 弧度）的水平视场和约 180°（π 或约 3.142 弧度）的垂直 FOV。

缩小摄像机的 FOV 会减少视口中包含的弧线，从而在渲染到视图时放大该内容。这与光学变焦效果存在差异，但结果通常足够接近以完成工作。

以下函数返回一个投影透视矩阵，该矩阵集成了指定的视场角以及给定的近裁剪面和远裁剪面距离

function createPerspectiveMatrix(viewport, fovDegrees, nearClip, farClip) {
  const fovRadians = fovDegrees * (Math.PI / 180.0);
  const aspectRatio = viewport.width / viewport.height;

  const transform = mat4.create();
  mat4.perspective(transform, fovRadians, aspectRatio, nearClip, farClip);
  return transform;
}

在将 FOV 角度 fovDegrees 从度转换为弧度并计算由 viewport 参数指定的 XRViewport 的纵横比之后，此函数使用 glMatrix 库的 mat4.perspective() 函数来计算透视矩阵。

透视矩阵将视野（技术上是垂直视野）、纵横比以及近远裁剪平面封装在 4x4 矩阵 transform 中，然后将其返回给调用者。

近裁剪面是到与显示表面平行的平面的距离（以米为单位），比该平面更近的任何东西都不会被绘制。位于该平面与摄像机同一侧的任何顶点都不会被绘制。相反，远裁剪面是到某个平面的距离（以米为单位），超出该平面后没有顶点被绘制。

要使用缩放因子或百分比进行缩放，您可以将 1 倍（正常大小的 100%）映射到您允许的最大 FOV 值（这会导致可见内容最多），然后将您的最大放大倍数映射到您支持的最大 FOV 值，并映射介于两者之间的相应值。

如果你在每一帧的渲染过程中都计算透视矩阵，那么你可以将所有其他需要应用的变换乘入该矩阵，以得到该帧所需的几何体。例如：

const transform = createPerspectiveMatrix(viewport, 130, 1, 100);
const translateVec = vec3.fromValues(
  -trackDistance,
  -craneDistance,
  pushDistance,
);
mat4.translate(transform, transform, translateVec);

这从一个表示 130° 垂直视场的透视矩阵开始，然后应用一个平移，以一种包含横向移动、升降和推入运动的方式移动摄像机。

缩放变换

与真正的“缩放”不同，缩放涉及将位置或顶点中的每个 x、y 和 z 坐标值乘以该轴的缩放因子。这些因子可能不一定对每个轴都相同，尽管最接近缩放效果的结果将涉及对每个轴使用相同的值。这需要应用于场景中的每个顶点——理想情况下是在顶点着色器中。

如果你想放大 2 倍，你需要将每个分量乘以 2.0。要缩小相同倍数，将它们乘以 -2.0。在矩阵术语中，这是通过将缩放因子考虑在内的变换矩阵来执行的，如下所示：

let scaleTransform = [
  Sx, 0, 0, 0,
  0, Sy, 0, 0,
  0, 0, Sz, 0,
  0, 0, 0, 1
];

此矩阵表示一个变换，其缩放因子由 (Sx, Sy, Sz) 表示，其中 Sx 表示沿 X 轴的缩放因子，Sy 表示沿 Y 轴的缩放因子，Sz 表示沿 Z 轴的缩放因子。如果这些值中的任何一个与其他值不同，则结果将是拉伸或收缩，其在某些维度上与其他维度不同。

如果每个方向都要应用相同的缩放因子，您可以创建一个简单的函数来为您生成缩放变换矩阵：

function createScalingMatrix(f) {
  return [f, 0, 0, 0, 0, f, 0, 0, 0, 0, f, 0, 0, 0, 0, 1];
}

有了变换矩阵，我们将变换 scaleTransform 应用于向量（或顶点）myVector

let myVector = [2, 1, -3];
let scaleTransform = [2, 0, 0, 0, 0, 2, 0, 0, 0, 0, 2, 0, 0, 0, 0, 1];
vec4.transformMat4(myVector, myVector, scaleTransform);

或者，使用上面所示的 createScalingMatrix() 函数，沿每个轴以相同的因子进行缩放

let myVector = [2, 1, -3];
vec4.transformMat4(myVector, myVector, createScalingMatrix(2.0));

平移（向左或向右偏航）

平移或偏航是摄像机左右旋转，其底座保持固定。摄像机在空间中的位置不变，只改变其看向的方向。而且该方向除了水平方向外不会改变。平移非常适合建立背景或在广阔的空间或巨大的物体上提供范围感。或者只是左右看，就像模拟玩家在沉浸式或 VR 场景中转动头部一样。

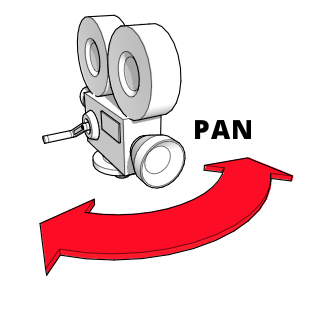
要做到这一点，我们需要围绕 Y 轴旋转，以模拟摄像机的左右旋转。使用我们之前使用过的 glMatrix 库，这可以通过 mat4 类上的 rotateY() 方法来完成，该类表示一个标准的 4x4 矩阵。要将由矩阵 viewMatrix 定义的视点旋转 panAngle 弧度：

mat4.rotateY(viewMatrix, viewMatrix, panAngle);

如果 panAngle 为正，此变换将使摄像机向右平移；如果 panAngle 为负，则向左平移。

倾斜（向上或向下俯仰）

当你倾斜或俯仰摄像机时，你将它固定在相同的空间坐标中，同时垂直改变它朝向的方向，而根本不改变其朝向的水平部分。它调整了它向上和向下指向的方向。倾斜对于捕捉高大物体或场景的范围很有用，例如森林或山脉，但也是引入重要或令人敬畏的人物或地点的一种流行方式。当然，它也有助于实现玩家上下看的支持。

因此，倾斜摄像机可以通过围绕 X 轴旋转摄像机来实现，使其向上和向下旋转。这可以使用矩阵数学库中的适当方法完成，例如 glMatrix 的 mat4 类中的 rotateX() 方法：

mat4.rotateX(viewMatrix, viewMatrix, angle);

angle 的正值将使摄像机向下倾斜，而 angle 的负值将使其向上倾斜。

推拉（向内或向外移动）

推拉镜头是指整个摄像机向前和向后移动的镜头。在经典电影制作中，这通常通过将摄像机安装在轨道上或移动车辆上来完成。由此产生的运动可以产生令人印象深刻的平滑效果，特别是当与您拍摄焦点的人物或物体一起移动时。

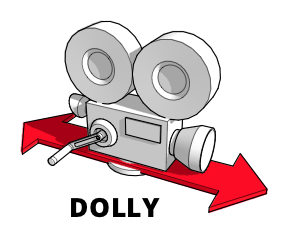
虽然推拉镜头和变焦镜头看起来应该差不多，但它们并不一样。变焦改变了摄像机的焦距，这意味着目标与其周围环境的空间关系不会改变，即使目标在画面中变大或变小。另一方面，推拉镜头通过实际移动摄像机，复制了物理运动的感觉，使场景中物体之间的关系在你朝着或远离拍摄目标移动时，按照你的预期发生变化。

要执行推拉操作，请沿 Z 轴向前和向后平移摄像机视图

mat4.translate(viewMatrix, viewMatrix, [0, 0, dollyDistance]);

此处，[0, 0, dollyDistance] 是一个向量，其中 dollyDistance 是摄像机推拉的距离。由于这是通过围绕摄像机移动整个世界来工作的，因此这里真正发生的是整个世界沿 Z 轴相对于摄像机移动 dollyDistance 米。如果 dollyDistance 为正，世界将向用户移动该量，导致摄像机更接近场景。相反，dollyDistance 的负值将世界移离用户，导致摄像机似乎向后移动远离目标。

跟拍（左右移动）

使用物理摄像机的跟拍与推拉使用相同的设备，但它不是向前和向后移动摄像机，而是左右移动或反之。摄像机完全不旋转，因此拍摄焦点会慢慢滑出画面。这可以在尝试在场景中建立情感时暗示专注、时间流逝或沉思。它也经常用于“边走边聊”的场景中，其中摄像机沿着角色滑动，角色穿过场景。

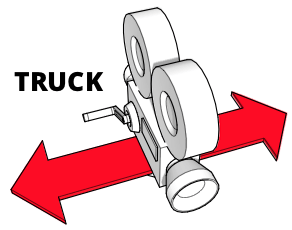
要左右移动摄像机，请沿 X 轴平移视图矩阵，方向与所需的摄像机移动方向相反

mat4.translate(viewMatrix, viewMatrix, [-truckDistance, 0, 0]);

请注意向量 [-truckDistance, 0, 0]。这补偿了跟拍操作是通过移动世界而不是摄像机来工作的事实。通过将整个世界移动到与 truckDistance 指示的方向相反的方向，我们实现了摄像机沿预期方向移动的效果。这样，truckDistance 的正值将使摄像机向右移动（通过向左移动世界），而 truckDistance 的负值将使摄像机向左移动（通过向右移动世界）。

升降（上下移动）

升降镜头是指摄像机相对于地面水平固定，但垂直上下移动的镜头。想象一下摄像机在一个基座（或杆）上，基座变得更高或更矮。这对于跟踪一个正在变高或变矮、或者从椅子上站起来或坐下、或者垂直上下移动的主体很有用。

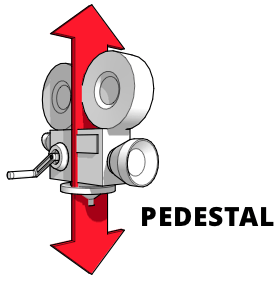
这类似于摇臂镜头，摇臂镜头涉及移动连接在摇臂上的摄像机上下。要执行升降或摇臂运动，请沿 Y 轴平移视图，方向与您想要移动摄像机的方向相反

mat4.translate(viewMatrix, viewMatrix, [0, -pedestalDistance, 0]);

通过对 pedestalDistance 的值取反，我们补偿了我们实际上正在移动世界而不是摄像机的事实。因此，pedestalDistance 的正值将使摄像机向上移动，而负值将使其向下移动。

倾斜（左右滚动）

倾斜（或滚动）是摄像机围绕其滚动轴的旋转；也就是说，摄像机固定在空间中，并保持指向同一位置，但旋转，使摄像机的顶部指向不同的方向。

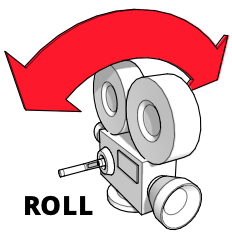
你可以这样想象：伸出你的手臂，手掌向下。想象你的手是摄像机，手背代表摄像机顶部。现在旋转你的手，使“摄像机”倒置。你刚刚将你的手围绕滚动轴倾斜了。在电影摄影中，倾斜可以用来模拟各种不稳定的运动，如波浪或湍流，但也可以用于戏剧效果。

使用 glMatrix 实现绕 Z 轴的旋转

mat4.rotateZ(viewMatrix, viewMatrix, cantAngle);

组合运动

您可以同时执行多种运动，例如在平移的同时缩放，或同时倾斜和倾斜。

沿多轴平移

沿多个轴进行平移非常简单。之前，我们是这样进行平移的：

mat4.translate(viewMatrix, viewMatrix, [-truckDistance, 0, 0]);
mat4.translate(viewMatrix, viewMatrix, [0, -pedestalDistance, 0]);
mat4.translate(viewMatrix, viewMatrix, [0, 0, dollyDistance]);

这里的解决方案很明显。由于平移表示为一个向量，提供了沿每个轴移动的距离，我们可以将它们组合起来，如下所示：

mat4.translate(viewMatrix, viewMatrix, [
  -truckDistance,
  -pedestalDistance,
  dollyDistance,
]);

这将使矩阵 viewMatrix 的原点沿每个轴移动指定的量。

围绕多个轴旋转

您还可以将围绕多个轴的旋转组合成围绕一个代表旋转的共享轴的四元数进行单一旋转。要单独执行旋转，您可以使用欧拉角（围绕每个轴的单独角度）来应用俯仰、偏航和滚动，如下所示：

mat4.rotateX(viewMatrix, viewMatrix, pitchAngle);
mat4.rotateY(viewMatrix, viewMatrix, yawAngle);
mat4.rotateZ(viewMatrix, viewMatrix, rollAngle);

您可以转而从欧拉角构造一个表示组合旋转轴的四元数，然后使用乘法旋转矩阵，如下所示：

const axisQuat = quat.create();
const rotateMatrix = mat4.create();
quat.fromEuler(axisQuat, pitchAngle, yawAngle, rollAngle);
mat4.fromQuat(rotateMatrix, axisQuat);
mat4.multiply(viewMatrix, viewMatrix, rotateMatrix);

这会将俯仰、偏航和滚动的欧拉角转换为表示所有三个旋转的四元数。然后将其转换为旋转变换矩阵；最后，视图矩阵乘以旋转变换以完成旋转。

用 WebXR 表示 3D

WebXR 将 3D 图形更进一步，允许使用特殊的视觉硬件（如护目镜或头戴设备）来呈现 3D 图形，这些图形似乎真实存在于三维空间中，可能在现实世界的背景下（在增强现实的情况下）。

为了感知深度，需要对场景有两个视角。通过比较这两个视图，可以识别物体的深度，并进一步识别观看者与所见物体之间的距离。这就是我们有两只眼睛，略微分开的原因。你可以通过一次闭上一只眼睛，然后交替切换两只眼睛来提醒自己这个事实。注意你的左眼如何能看到鼻子的左侧而不是右侧，而你的右眼能看到鼻子的右侧而不是左侧。这只是你的每只眼睛所看到内容之间众多差异之一。

我们的大脑接收到两组关于我们视野内光照水平和波长的数据——每只眼睛一组。大脑利用这些数据在我们的脑海中构建场景，利用两个视角之间的微小差异来计算深度和距离。

渲染场景

XR——涵盖虚拟现实 (VR) 和增强现实 (AR) 的简称——头戴设备通过绘制场景的两个视图向我们呈现 3D 图像，这两个视图略微偏移，就像我们两只眼睛获得的视图一样。然后将这些视图分别提供给每只眼睛，以便它们收集我们大脑构建 3D 图像所需的数据。

为此，WebXR 要求您的渲染器为每一帧视频绘制场景两次——每只眼睛一次。这两个视图渲染到同一个帧缓冲区中，一个在左侧，一个在右侧。然后 XR 设备使用屏幕和透镜将生成的图像的左半部分呈现给我们的左眼，将右半部分呈现给我们的右眼。

例如，考虑一个使用 2560x1440 像素帧缓冲区的设备。将其分为两部分——每只眼睛一半——导致每只眼睛的视图以 1280x1440 像素的分辨率绘制。从概念上讲，它看起来是这样的：

您的代码通过调用 XRSession 方法 requestAnimationFrame() 来告知 WebXR 引擎您想要提供下一帧动画，并提供一个渲染动画帧的回调函数。当浏览器需要您渲染场景时，它会调用回调，将当前时间和一个 XRFrame（封装渲染正确帧所需的数据）作为输入参数提供。

此信息包括描述观看者在场景中位置和朝向方向的 XRViewerPose，以及 XRView 对象的列表，每个对象代表场景的一个视角。在当前的 WebXR 实现中，此列表中永远不会有超过两个条目：一个描述左眼的位置和视角，另一个描述右眼的位置和视角。您可以通过检查给定 XRView 的 eye 属性的值来判断它代表哪只眼睛，该属性是一个字符串，其值为 left 或 right（第三个可能的值 none 理论上可用于表示另一个视角，但当前 API 中对此的支持并不完全可用）。

帧回调示例

一个相当基本（但典型）的帧渲染回调可能看起来像这样：

function myAnimationFrameCallback(time, frame) {
  const adjustedRefSpace = applyPositionOffsets(xrReferenceSpace);
  const pose = frame.getViewerPose(adjustedRefSpace);

  animationFrameRequestID = frame.session.requestAnimationFrame(
    myAnimationFrameCallback,
  );

  if (pose) {
    const glLayer = frame.session.renderState.baseLayer;
    gl.bindFramebuffer(gl.FRAMEBUFFER, glLayer.framebuffer);
    CheckGLError("Binding the framebuffer");

    gl.clearColor(0, 0, 0, 1.0);
    gl.clearDepth(1.0);
    gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
    CheckGLError("Clearing the framebuffer");

    const deltaTime = (time - lastFrameTime) * 0.001;
    lastFrameTime = time;

    for (const view of pose.views) {
      const viewport = glLayer.getViewport(view);
      gl.viewport(viewport.x, viewport.y, viewport.width, viewport.height);
      CheckGLError(`Setting viewport for eye: ${view.eye}`);

      myRenderScene(gl, view, sceneData, deltaTime);
    }
  }
}

回调开始时调用一个自定义函数 applyPositionOffsets()，该函数接收一个参考空间，并对其变换矩阵应用任何需要进行的更改，以考虑诸如 WebXR 未控制的设备（如键盘和鼠标）的用户输入等因素。此函数返回的调整后的 XRReferenceSpace 然后传递给 XRFrame 方法 getViewerPose() 以获取表示观看者位置和视角的 XRViewerPose。

接下来，我们继续排队请求渲染下一帧视频，这样我们就不必担心稍后再做，通过再次调用 requestAnimationFrame()。

现在是渲染场景的时候了。如果我们成功获取到姿态，我们就会从会话的 renderState 对象的 baseLayer 属性中获取渲染所需的 XRWebGLLayer。我们使用 WebGLRenderingContext 方法 gl.bindFrameBuffer() 将其绑定到 WebGL 的 gl.FRAMEBUFFER 目标。

然后我们清空帧缓冲区，以确保我们从已知状态开始，因为我们的渲染器不会触及每个像素。我们使用 gl.clearColor() 将清除颜色设置为不透明黑色，并通过调用 WebGLRenderingContext 方法 gl.clearDepth() 将深度缓冲区清除的值设置为 1.0。然后我们调用 WebGLRenderingContext 方法 gl.clear()，它会清除帧缓冲区（因为我们在掩码参数中包含了 gl.COLOR_BUFFER_BIT）和深度缓冲区（因为我们包含了 gl.DEPTH_BUFFER_BIT）。

然后，我们通过比较帧的所需渲染时间与上一帧的绘制时间，来确定自上一帧渲染以来经过了多少时间。由于此值以毫秒为单位，我们通过乘以 0.001（或除以 1000）将其转换为秒。

现在我们循环遍历姿态的视图，这些视图可以在 XRViewerPose 数组 views 中找到。对于每个视图，我们向 XRWebGLLayer 请求要使用的适当视口，通过将位置和大小信息传递给 gl.viewport() 来配置 WebGL 视口以匹配。这限制了渲染，使我们只能绘制到帧缓冲区中代表由 view.eye 标识的眼睛所看到的图像的部分。

在建立这些约束条件并准备好所有其他所需内容后，我们调用一个自定义函数 myRenderScene() 来实际执行计算和 WebGL 渲染以渲染帧。在这种情况下，我们传入 WebGL 上下文 gl、XRView view、一个 sceneData 对象（其中包含顶点和片段着色器、顶点列表、纹理等内容），以及 deltaTime，它指示自上一帧以来经过的时间，以便我们知道动画应该前进多远。

当此函数返回时，WebXR 正在使用的 WebGL 帧缓冲区中现在包含场景的两个副本，每个副本占据帧的一半：一个用于左眼，一个用于右眼。这些副本通过 XR 软件和驱动程序进入头戴设备，其中每一半都显示给相应的眼睛。

另见

• 几何和参考空间
• WebGL 模型视图投影
• 用于 Web 的矩阵数学
• 移动、方向和运动：一个 WebXR 示例