1. Web
  2. Web API
  3. WebGL: 网页的 2D 和 3D 图形
  4. WebGL 模型视图投影

WebGL 模型视图投影

本文探讨如何在 WebGL 项目中获取数据，并将其投影到适当的空间以显示在屏幕上。它假设读者了解使用平移、缩放和旋转矩阵进行基本矩阵数学运算的知识。它解释了在组合 3D 场景时通常使用的三个核心矩阵：模型矩阵、视图矩阵和投影矩阵。

模型矩阵、视图矩阵和投影矩阵

WebGL 中点和多边形在空间中的单独变换由基本的变换矩阵（如平移、缩放和旋转）处理。这些矩阵可以组合在一起，并以特殊方式分组，以便它们可用于渲染复杂的 3D 场景。这些组合矩阵最终将原始模型数据移动到名为裁剪空间的特殊坐标空间中。这是一个 2 个单位宽的立方体，以 (0,0,0) 为中心，角点范围从 (-1,-1,-1) 到 (1,1,1)。这个裁剪空间被压缩成 2D 空间并光栅化成图像。

下面讨论的第一个矩阵是模型矩阵，它定义了如何获取原始模型数据并在 3D 世界空间中移动它。投影矩阵用于将世界空间坐标转换为裁剪空间坐标。一个常用的投影矩阵，即透视投影矩阵，用于模拟典型相机作为 3D 虚拟世界中观察者的效果。视图矩阵负责移动场景中的对象，以模拟相机位置的变化，从而改变观察者当前能够看到的内容。

以下部分深入探讨了模型矩阵、视图矩阵和投影矩阵背后的思想和实现。这些矩阵是数据在屏幕上移动的核心，并且是超越单个框架和引擎的概念。

裁剪空间

在 WebGL 程序中，数据通常以其自己的坐标系上传到 GPU，然后顶点着色器将这些点转换成一个称为裁剪空间的特殊坐标系。任何超出裁剪空间的数据都将被裁剪掉，不予渲染。但是，如果一个三角形横跨此空间的边界，则它将被分割成新的三角形，并且只保留新三角形在裁剪空间中的部分。

A 3d graph showing clip space in WebGL.

上面的图形是所有点必须适合的裁剪空间的可视化。它是一个边长为两个单位的立方体，一个角在 (-1,-1,-1)，对角在 (1,1,1)。立方体的中心是点 (0,0,0)。裁剪空间使用的这个 8 立方米的坐标系称为归一化设备坐标 (NDC)。你在研究和使用 WebGL 代码时可能会不时遇到这个术语。

对于本节，我们将直接将数据放入裁剪坐标系。通常使用任意坐标系中的模型数据，然后使用矩阵对其进行变换，将模型坐标转换为裁剪空间坐标系。对于这个示例，最容易通过使用范围从 (-1,-1,-1) 到 (1,1,1) 的模型坐标值来说明裁剪空间的工作原理。下面的代码将创建 2 个三角形，它们将在屏幕上绘制一个正方形。正方形中的 Z 深度决定了当正方形共享相同空间时哪个被绘制在上面。较小的 Z 值被渲染在较大的 Z 值之上。

WebGLBox 示例

此示例将创建一个自定义的 WebGLBox 对象，它将在屏幕上绘制一个 2D 框。它被实现为一个类，其中包含一个构造函数和一个 draw() 方法来在屏幕上绘制一个框。

js
class WebGLBox {
  canvas = document.getElementById("canvas");
  gl = this.canvas.getContext("webgl");
  webglProgram = createWebGLProgramFromIds(
    this.gl,
    "vertex-shader",
    "fragment-shader",
  );
  positionLocation;
  colorLocation;
  constructor() {
    const gl = this.gl;

    // Setup a WebGL program
    gl.useProgram(this.webglProgram);

    // Save the attribute and uniform locations
    this.positionLocation = gl.getAttribLocation(this.webglProgram, "position");
    this.colorLocation = gl.getUniformLocation(this.webglProgram, "vColor");

    // Tell WebGL to test the depth when drawing, so if a square is behind
    // another square it won't be drawn
    gl.enable(gl.DEPTH_TEST);
  }
  draw(settings) {
    // Create some attribute data; these are the triangles that will end being
    // drawn to the screen. There are two that form a square.

    // prettier-ignore
    const data = new Float32Array([
      // Triangle 1
      settings.left, settings.bottom, settings.depth,
      settings.right, settings.bottom, settings.depth,
      settings.left, settings.top, settings.depth,

      // Triangle 2
      settings.left, settings.top, settings.depth,
      settings.right, settings.bottom, settings.depth,
      settings.right, settings.top, settings.depth,
    ]);

    // Use WebGL to draw this onto the screen.

    // Performance Note: Creating a new array buffer for every draw call is slow.
    // This function is for illustration purposes only.

    const gl = this.gl;

    // Create a buffer and bind the data
    const buffer = gl.createBuffer();
    gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
    gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);

    // Setup the pointer to our attribute data (the triangles)
    gl.enableVertexAttribArray(this.positionLocation);
    gl.vertexAttribPointer(this.positionLocation, 3, gl.FLOAT, false, 0, 0);

    // Setup the color uniform that will be shared across all triangles
    gl.uniform4fv(this.colorLocation, settings.color);

    // Draw the triangles to the screen
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }
}

着色器是使用 GLSL 编写的代码片段，它们获取我们的数据点并最终将它们渲染到屏幕上。为方便起见，这些着色器存储在 <script> 元素中，并通过自定义函数 createWebGLProgramFromIds() 引入程序。此函数处理获取一些 GLSL 源代码并将其编译为 WebGL 程序的基本操作。它需要三个参数——渲染程序的上下文、包含顶点着色器的 <script> 元素的 ID，以及包含片段着色器的 <script> 元素的 ID。此函数在此处不详细解释；如果你想查看其实现，请点击代码块上的“播放”。顶点着色器定位顶点，片段着色器为每个像素着色。

首先看一下将在屏幕上移动顶点的顶点着色器

glsl
// The individual position vertex
attribute vec3 position;

void main() {
  // the gl_Position is the final position in clip space after the vertex shader modifies it
  gl_Position = vec4(position, 1.0);
}

接下来，要将数据实际光栅化为像素，片段着色器以每个像素为基础评估所有内容，并设置单个颜色。GPU 为它需要渲染的每个像素调用着色器函数；着色器的任务是返回用于该像素的颜色。

glsl
precision mediump float;
uniform vec4 vColor;

void main() {
  gl_FragColor = vColor;
}

包含这些设置后，是时候直接使用裁剪空间坐标绘制到屏幕了。

js
const box = new WebGLBox();

首先在中间绘制一个红色框。

js
box.draw({
  top: 0.5, // x
  bottom: -0.5, // x
  left: -0.5, // y
  right: 0.5, // y

  depth: 0, // z
  color: [1, 0.4, 0.4, 1], // red
});

接下来，在红色框的上方和后面绘制一个绿色框。

js
box.draw({
  top: 0.9, // x
  bottom: 0, // x
  left: -0.9, // y
  right: 0.9, // y

  depth: 0.5, // z
  color: [0.4, 1, 0.4, 1], // green
});

最后，为了演示裁剪确实正在发生，此框未被绘制，因为它完全超出裁剪空间。深度超出 -1.0 到 1.0 的范围。

js
box.draw({
  top: 1, // x
  bottom: -1, // x
  left: -1, // y
  right: 1, // y

  depth: -1.5, // z
  color: [0.4, 0.4, 1, 1], // blue
});

结果

练习

此时一个有用的练习是移动裁剪空间中的框，通过改变代码来感受点如何在裁剪空间中被裁剪和移动。尝试绘制一个像带背景的方块笑脸的图片。

齐次坐标

前一个裁剪空间顶点着色器的主要行包含此代码

glsl
gl_Position = vec4(position, 1.0);

position 变量在 draw() 方法中定义，并作为属性传递到着色器。这是一个三维点，但最终通过管道传递的 gl_Position 变量实际上是四维的——不是 (x, y, z)，而是 (x, y, z, w)。z 之后没有字母，因此按照惯例，这个第四维度标记为 w。在上面的示例中，w 坐标设置为 1.0。

显而易见的问题是“为什么多了一个维度？”事实证明，这个附加维度允许许多操纵 3D 数据的好技术。这个附加维度将透视概念引入坐标系；有了它，我们可以将 3D 坐标映射到 2D 空间——从而允许两条平行线在它们向远处后退时相交。w 的值用作坐标其他分量的除数，因此 x、y 和 z 的真实值计算为 x/w、y/w 和 z/w（然后 w 也成为 w/w，变为 1）。

一个三维点在典型的笛卡尔坐标系中定义。添加的第四维将此点更改为齐次坐标。它仍然代表 3D 空间中的一个点，并且可以很容易地通过一对简单函数演示如何构造这种类型的坐标。

js
function cartesianToHomogeneous(point) {
  let x = point[0];
  let y = point[1];
  let z = point[2];

  return [x, y, z, 1];
}

function homogeneousToCartesian(point) {
  let x = point[0];
  let y = point[1];
  let z = point[2];
  let w = point[3];

  return [x / w, y / w, z / w];
}

如前所述，并在上述函数中所示，w 分量除以 x、y 和 z 分量。当 w 分量是非零实数时，齐次坐标很容易转换回笛卡尔空间中的正常点。现在，如果 w 分量为零会发生什么？在 JavaScript 中，返回的值将如下所示。

js
homogeneousToCartesian([10, 4, 5, 0]);

这等于：[Infinity, Infinity, Infinity]。

此齐次坐标表示无穷远处的某个点。这是一种方便地表示从原点沿特定方向射出的光线的方法。除了光线之外，它还可以被认为是方向向量的表示。如果此齐次坐标与带有平移的矩阵相乘，则平移实际上被去除。

当计算机上的数字非常大（或非常小）时，它们会变得越来越不精确，因为用于表示它们的 1 和 0 的数量有限。对较大数字执行的操作越多，结果中积累的错误就越多。当除以 w 时，这可以通过对两个可能较小、较不易出错的数字进行操作来有效地提高非常大数字的精度。

使用齐次坐标的最后一个好处是它们非常适合与 4x4 矩阵相乘。顶点必须至少匹配矩阵的一个维度才能与之相乘。4x4 矩阵可用于编码各种有用的变换。实际上，典型的透视投影矩阵使用 w 分量的除法来实现其变换。

裁剪空间中点和多边形的裁剪发生在齐次坐标转换回笛卡尔坐标（通过除以 w）之前。这个最终空间被称为归一化设备坐标或 NDC。

要开始尝试这个想法，可以修改之前的示例以允许使用 w 分量。除了修改 data，还要记住将 vertexAttribPointer() 更改为使用 4 个分量（第二个 size 参数）而不是 3 个。

js
// Redefine the triangles to use the W component
// prettier-ignore
const data = new Float32Array([
  // Triangle 1
  settings.left, settings.bottom, settings.depth, settings.w,
  settings.right, settings.bottom, settings.depth, settings.w,
  settings.left, settings.top, settings.depth, settings.w,

  // Triangle 2
  settings.left, settings.top, settings.depth, settings.w,
  settings.right, settings.bottom, settings.depth, settings.w,
  settings.right, settings.top, settings.depth, settings.w,
]);

然后顶点着色器使用传入的 4 维点。

glsl
attribute vec4 position;

void main() {
  gl_Position = position;
}

首先，我们在中间绘制一个红色框，但将 W 设置为 0.7。当坐标除以 0.7 时，它们都将被放大。

js
box.draw({
  top: 0.5, // y
  bottom: -0.5, // y
  left: -0.5, // x
  right: 0.5, // x
  w: 0.7, // w - enlarge this box

  depth: 0, // z
  color: [1, 0.4, 0.4, 1], // red
});

现在，我们在上方绘制一个绿色框，但通过将 w 分量设置为 1.1 来缩小它。

js
box.draw({
  top: 0.9, // y
  bottom: 0, // y
  left: -0.9, // x
  right: 0.9, // x
  w: 1.1, // w - shrink this box

  depth: 0.5, // z
  color: [0.4, 1, 0.4, 1], // green
});

最后一个框未被绘制，因为它超出裁剪空间。深度超出 -1.0 到 1.0 的范围。

js
box.draw({
  top: 1, // y
  bottom: -1, // y
  left: -1, // x
  right: 1, // x
  w: 1.5, // w - Bring this box into range

  depth: -1.5, // z
  color: [0.4, 0.4, 1, 1], // blue
});

结果

练习

  • 尝试这些值，看看它们如何影响屏幕上渲染的内容。请注意，通过设置蓝色框的 w 分量，之前被裁剪的蓝色框如何重新回到范围内。
  • 尝试创建一个超出裁剪空间的新框，并通过除以 w 将其带回。

模型变换

直接将点放置在裁剪空间中的用途有限。在实际应用中，你不会所有源坐标都已经位于裁剪空间坐标中。因此，大多数情况下，你需要将模型数据和其他坐标转换到裁剪空间。简单的立方体是说明如何做到这一点的一个简单示例。立方体数据由顶点位置、立方体面的颜色以及构成单个多边形的顶点位置顺序（以 3 个顶点为一组来构建组成立方体面的三角形）组成。位置和颜色存储在 GL 缓冲区中，作为属性发送到着色器，然后单独进行操作。

最后计算并设置单个模型矩阵。此矩阵表示对构成模型的每个点执行的变换，以便将其移动到正确的空间，并对模型中的每个点执行任何其他所需的变换。这不仅适用于每个顶点，还适用于模型每个表面上的每个点。

在这种情况下，对于动画的每一帧，一系列缩放、旋转和平移矩阵将数据移动到裁剪空间中的所需位置。立方体的大小与裁剪空间相同（从 -1,-1,-1 到 1,1,1），因此需要将其缩小，以免完全填充裁剪空间。此矩阵在 JavaScript 中预先乘法后直接发送到着色器。

以下代码示例定义了 CubeDemo 对象上的一个方法，该方法将创建模型矩阵。新函数看起来像这样（实用函数在Web 的矩阵数学章节中介绍）

js
function computeModelMatrix(now) {
  // Scale down by 20%
  const scaleMatrix = scale(0.2, 0.2, 0.2);
  // Rotate a slight tilt
  const rotateXMatrix = rotateX(now * 0.0003);
  // Rotate according to time
  const rotateYMatrix = rotateY(now * 0.0005);
  // Move slightly down
  const translateMatrix = translate(0, -0.1, 0);
  // Multiply together, make sure and read them in opposite order
  this.transforms.model = multiplyArrayOfMatrices([
    translateMatrix, // step 4
    rotateYMatrix, // step 3
    rotateXMatrix, // step 2
    scaleMatrix, // step 1
  ]);
}

为了在着色器中使用它，它必须设置为统一位置。统一变量的位置保存在下面所示的 locations 对象中。

js
this.locations.model = gl.getUniformLocation(webglProgram, "model");

最后将统一变量设置到该位置。这将矩阵传递给 GPU。

js
gl.uniformMatrix4fv(
  this.locations.model,
  false,
  new Float32Array(this.transforms.model),
);

在着色器中，每个位置顶点首先被转换成齐次坐标（一个 vec4 对象），然后与模型矩阵相乘。

glsl
gl_Position = model * vec4(position, 1.0);

注意：在 JavaScript 中，矩阵乘法需要自定义函数，而在着色器中，它内置于语言中，使用简单的 * 运算符。

完整的编排代码是隐藏的。同样，如果你感兴趣，请点击本节中代码块上的“播放”查看。

结果

此时，变换后的点的 w 值仍然是 1.0。立方体仍然没有任何透视。下一节将采用此设置并修改 w 值以提供一些透视。

练习

  • 使用缩放矩阵缩小框，并将其放置在裁剪空间中的不同位置。
  • 尝试将其移出裁剪空间。
  • 调整窗口大小，观察框如何变形。
  • 添加 rotateZ 矩阵。

除以 W

要开始对我们的立方体模型获得一些透视效果，一个简单的方法是将 Z 坐标复制到 w 坐标。通常，当将笛卡尔点转换为齐次坐标时，它会变成 (x,y,z,1)，但我们将其设置为类似于 (x,y,z,z)。实际上，我们希望确保视图中的点 z 大于 0，因此我们将通过将值更改为 ((1.0 + z) * scaleFactor) 进行轻微修改。这将使通常在裁剪空间中（-1 到 1）的点根据比例因子设置移动到更像（0 到 1）的空间。比例因子会改变最终的 w 值，使其整体更高或更低。

着色器代码如下所示。

glsl
// First transform the point
vec4 transformedPosition = model * vec4(position, 1.0);

// How much effect does the perspective have?
float scaleFactor = 0.5;

// Set w by taking the z value which is typically ranged -1 to 1, then scale
// it to be from 0 to some number, in this case 0-1.
float w = (1.0 + transformedPosition.z) * scaleFactor;

// Save the new gl_Position with the custom w component
gl_Position = vec4(transformedPosition.xyz, w);

结果

看到那个面向摄像机的小三角形了吗？这是它出现时的截图。

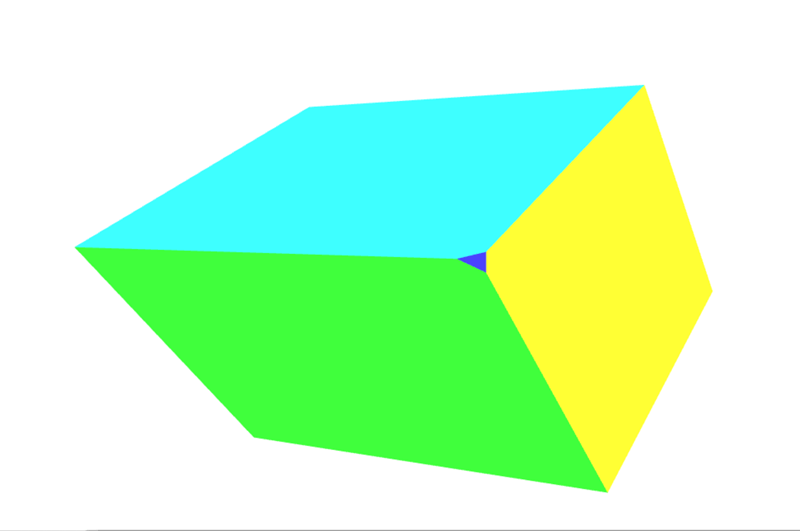
A small triangle appears in the top right corner

这是我们对象上添加的另一个面，因为我们形状的旋转导致该角延伸到裁剪空间之外，从而导致该角被裁剪掉。有关如何使用更复杂的矩阵来帮助控制和防止裁剪的介绍，请参阅下面的透视投影矩阵。

练习

如果这听起来有点抽象，打开顶点着色器并调整比例因子，看看它如何使顶点更多地向表面收缩。完全改变 w 分量的值，以获得真正奇特的空间表示。

在下一节中，我们将把 Z 复制到 w 插槽的这一步变成一个矩阵。

简单投影

填充 w 分量的最后一步实际上可以通过一个简单的矩阵来完成。从单位矩阵开始。

js
// prettier-ignore
const identity = [
  1, 0, 0, 0,
  0, 1, 0, 0,
  0, 0, 1, 0,
  0, 0, 0, 1,
];

multiplyPoint(identity, [2, 3, 4, 1]);
// [2, 3, 4, 1]

然后将最后一列的 1 向上移动一个位置。

js
// prettier-ignore
const copyZ = [
  1, 0, 0, 0,
  0, 1, 0, 0,
  0, 0, 1, 1,
  0, 0, 0, 0,
];

multiplyPoint(copyZ, [2, 3, 4, 1]);
// [2, 3, 4, 4]

然而，在最后一个例子中，我们执行了 (z + 1) * scaleFactor。

js
const scaleFactor = 0.5;

// prettier-ignore
const simpleProjection = [
  1, 0, 0, 0,
  0, 1, 0, 0,
  0, 0, 1, scaleFactor,
  0, 0, 0, scaleFactor,
];

multiplyPoint(simpleProjection, [2, 3, 4, 1]);
// [2, 3, 4, 2.5]

再进一步分解一下，我们可以看到这是如何工作的。

js
const x = 2 * 1 + 3 * 0 + 4 * 0 + 1 * 0;
const y = 2 * 0 + 3 * 1 + 4 * 0 + 1 * 0;
const z = 2 * 0 + 3 * 0 + 4 * 1 + 1 * 0;
const w = 2 * 0 + 3 * 0 + 4 * scaleFactor + 1 * scaleFactor;

最后一行可以简化为

js
const w = 4 * scaleFactor + 1 * scaleFactor;

然后提取 scaleFactor，我们得到这个

js
const w = (4 + 1) * scaleFactor;

这与我们上一个例子中使用的 (z + 1) * scaleFactor 完全相同。

在立方体演示中，添加了一个额外的 computeSimpleProjectionMatrix() 方法。该方法在 draw() 方法中被调用，并将比例因子传递给它。结果应该与上一个示例相同。

js
function computeSimpleProjectionMatrix(scaleFactor) {
  // prettier-ignore
  this.transforms.projection = [
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, scaleFactor,
    0, 0, 0, scaleFactor,
  ];
}

尽管结果相同，但这里的重要步骤在顶点着色器中。它不是直接修改顶点，而是乘以一个额外的投影矩阵，它（顾名思义）将 3D 点投影到 2D 绘图表面。

glsl
// Make sure to read the transformations in reverse order
gl_Position = projection * model * vec4(position, 1.0);

结果

视锥体

在我们继续讨论如何计算透视投影矩阵之前，我们需要引入视锥体（也称为视图截锥体）的概念。这是当前用户可见的空间区域。它是由视野以及指定为最近和最远应渲染内容距离定义的 3D 空间区域。

在渲染时，我们需要确定哪些多边形需要渲染以表示场景。这就是视锥体所定义的。但视锥体到底是什么？

截锥体是将任何实体用两个平行平面切掉两个部分后形成的 3D 实体。考虑我们的相机，它正在查看一个从镜头正前方开始并延伸到远处的区域。可见区域是一个四面金字塔，其顶点位于镜头处，其四边对应于其周边视觉范围的范围，其底部位于它能看到的最远距离处，就像这样：

A depiction of the entire viewing area of a camera. This area is a four-sided pyramid with its peak at the lens and its base at the world's maximum viewable distance.

如果我们将此用于确定每帧要渲染的多边形，我们的渲染器将需要渲染此金字塔内的每个多边形，一直到无穷远，包括那些非常靠近镜头——可能太近而无用（当然包括那些如此之近以至于真实人类无法在同一设置中聚焦的东西）——的多边形。

所以减少我们需要计算和渲染的多边形数量的第一步，我们将这个金字塔变成视锥体。我们将用来切除顶点以减少多边形数量的两个平面是近裁剪平面和远裁剪平面。

在 WebGL 中，近裁剪平面和远裁剪平面是通过指定从镜头到垂直于视线的平面上最近点的距离来定义的。任何比近裁剪平面更靠近镜头或比远裁剪平面更远的东西都将被移除。这导致了视锥体，它看起来像这样：

A depiction of the camera's view frustum; the near and far planes have removed part of the volume, reducing the polygon count.

每帧要渲染的对象集基本上是通过从场景中所有对象的集合开始创建的。然后将完全在视锥体之外的任何对象从集合中移除。接下来，部分伸出视锥体之外的对象通过丢弃完全在视锥体之外的任何多边形，以及裁剪穿过视锥体外部的多边形，使其不再超出视锥体，从而被裁剪。

完成这些后，我们就有了完全在视锥体内的最大多边形集。这个列表通常会通过背面剔除（移除背面朝向相机的多边形）和使用隐藏表面判定的遮挡剔除（移除因为被更靠近镜头的多边形完全遮挡而无法看到的多边形）等过程进一步减少。

透视投影矩阵

到目前为止，我们已经一步步地建立了自己的 3D 渲染设置。然而，我们目前构建的代码存在一些问题。首先，每当我们调整窗口大小时，它都会变形。另一个问题是我们的简单投影无法处理场景数据的广泛值范围。大多数场景无法在裁剪空间中工作。定义与场景相关的距离将有助于避免在转换数字时丢失精度。最后，能够精确控制哪些点放置在裁剪空间内部和外部非常有用。在之前的示例中，立方体的角偶尔会被裁剪掉。

透视投影矩阵是一种投影矩阵，它满足所有这些要求。其数学运算也开始变得更复杂，并且不会在这些示例中完全解释。简而言之，它结合了除以 w（如之前的示例所示）和基于相似三角形的一些巧妙操作。如果你想阅读其背后数学的完整解释，请查看以下链接：

关于下面使用的透视投影矩阵，一个重要的注意事项是它翻转了 z 轴。在裁剪空间中，z+ 远离观察者，而使用此矩阵时，它向观察者靠近。

翻转 z 轴的原因是裁剪空间坐标系是左手坐标系（其中 z 轴指向远离观察者并进入屏幕），而数学、物理和 3D 建模以及 OpenGL 中的视图/眼睛坐标系的惯例是使用右手坐标系（z 轴指向屏幕外并朝向观察者）。更多信息请参阅相关维基百科文章：笛卡尔坐标系、右手定则。

让我们看看 perspective() 函数，它计算透视投影矩阵。

js
function perspective(fieldOfViewInRadians, aspectRatio, near, far) {
  const f = 1.0 / Math.tan(fieldOfViewInRadians / 2);
  const rangeInv = 1 / (near - far);

  // prettier-ignore
  return [
    f / aspectRatio, 0, 0, 0,
    0, f, 0, 0,
    0, 0, (near + far) * rangeInv, -1,
    0, 0, near * far * rangeInv * 2, 0,
  ];
}

此函数的四个参数是

fieldOfViewInRadians（视场角，以弧度表示）

一个以弧度表示的角度，指示观察者一次可以看到多少场景。数字越大，相机可见的越多。边缘的几何形状变得越来越扭曲，相当于一个广角镜头。当视场角越大时，物体通常会变小。当视场角越小，相机在场景中看到的就越少。物体受透视的影响扭曲得更少，物体看起来更接近相机。

aspectRatio

场景的纵横比，相当于其宽度除以其高度。在这些示例中，它是窗口宽度除以窗口高度。此参数的引入最终解决了画布调整大小和重塑时模型变形的问题。

nearClippingPlaneDistance

一个正数，表示屏幕内到垂直于地面的平面的距离，任何比此平面更近的物体都将被裁剪掉。这在裁剪空间中映射为 -1，不应设置为 0。

farClippingPlaneDistance

一个正数，表示超出此平面几何体将被裁剪掉的距离。这在裁剪空间中映射为 1。此值应保持与几何体距离合理接近，以避免渲染时出现精度误差。

在最新版本的立方体演示中，computeSimpleProjectionMatrix() 方法已被 computePerspectiveMatrix() 方法替换。

js
function computePerspectiveMatrix() {
  const fieldOfViewInRadians = Math.PI * 0.5;
  const aspectRatio = window.innerWidth / window.innerHeight;
  const nearClippingPlaneDistance = 1;
  const farClippingPlaneDistance = 50;

  this.transforms.projection = perspective(
    fieldOfViewInRadians,
    aspectRatio,
    nearClippingPlaneDistance,
    farClippingPlaneDistance,
  );
}

着色器代码与之前的示例相同。

glsl
gl_Position = projection * model * vec4(position, 1.0);

此外（未显示），模型的位移和缩放矩阵已更改，以将其移出裁剪空间并进入更大的坐标系。

结果

练习

  • 试验透视投影矩阵和模型矩阵的参数。
  • 将透视投影矩阵替换为使用正交投影。在 MDN WebGL 共享代码中，你会找到 MDN.orthographicMatrix()。这可以替换 CubeDemo.prototype.computePerspectiveMatrix() 中的 MDN.perspectiveMatrix() 函数。

视图矩阵

虽然一些图形库有一个可以在组合场景时定位和指向的虚拟摄像机，但 OpenGL（以及 WebGL）没有。这就是视图矩阵发挥作用的地方。它的任务是平移、旋转和缩放场景中的对象，以便它们相对于观察者（给定观察者的位置和方向）位于正确的位置。

模拟相机

这利用了爱因斯坦狭义相对论的一个基本方面：参照系和相对运动原理指出，从观察者的角度来看，你可以通过对场景中的对象施加相反的变化来模拟改变观察者的位置和方向。无论哪种方式，结果对观察者来说都是相同的。

想象一个盒子放在桌子上，一个相机放在离盒子一米远的地方，对准盒子，盒子的正面朝向相机。然后想象将相机移离盒子，直到它两米远（通过在相机的 Z 位置上增加一米），然后将其向左滑动 10 厘米。盒子从相机处后退这么多，并稍微向右滑动，从而在相机看来变小，并向相机暴露其左侧的一小部分。

现在让我们重置场景，将盒子放回其起始位置，相机距盒子两米远，并直接面向盒子。然而，这次相机被固定在桌子上，无法移动或转动。这就是 WebGL 中的工作方式。那么我们如何模拟相机在空间中的移动呢？

我们不是将相机向后和向左移动，而是对盒子应用逆变换：我们将盒子向后移动一米，然后向右移动 10 厘米。从这两个对象的角度来看，结果是相同的。

所有这些的最后一步是创建视图矩阵，它转换场景中的对象，使它们定位以模拟相机的当前位置和方向。我们现有的代码可以在世界空间中移动立方体并投影所有内容以具有透视，但我们仍然无法移动相机。

想象一下用物理相机拍摄电影。你拥有几乎可以随意放置相机并向任何方向瞄准相机的自由。为了在 3D 图形中模拟这一点，我们使用视图矩阵来模拟物理相机的位置和旋转。

与直接变换模型顶点的模型矩阵不同，视图矩阵移动的是一个抽象的相机。实际上，顶点着色器仍然只移动模型，而“相机”保持不动。为了使其正常工作，必须使用变换矩阵的逆矩阵。逆矩阵实际上是反转变换，所以如果我们向前移动相机视图，逆矩阵会导致场景中的物体向后移动。

以下 computeViewMatrix() 方法通过向内和向外、向左和向右移动视图矩阵来对其进行动画处理。

js
function computeViewMatrix(now) {
  const moveInAndOut = 20 * Math.sin(now * 0.002);
  const moveLeftAndRight = 15 * Math.sin(now * 0.0017);

  // Move the camera around
  const position = translate(moveLeftAndRight, 0, 50 + moveInAndOut);

  // Multiply together, make sure and read them in opposite order
  this.transforms.view = multiplyArrayOfMatrices([
    // Exercise: rotate the camera view
    position,
  ]);
}

着色器现在使用三个矩阵。

glsl
gl_Position = projection * view * model * vec4(position, 1.0);

在此步骤之后，GPU 管道将裁剪超出范围的顶点，并将模型发送到片段着色器进行光栅化。

结果

关联坐标系

此时，退一步看看并标记我们使用的各种坐标系将是有益的。首先，立方体的顶点在模型空间中定义。为了在场景中移动模型。这些顶点需要通过应用模型矩阵转换为世界空间。

模型空间 → 模型矩阵 → 世界空间

相机还没有做任何事情，这些点需要再次移动。目前它们在世界空间中，但需要将它们移动到视图空间（使用视图矩阵）以表示相机放置。

世界空间 → 视图矩阵 → 视图空间

最后，需要添加一个投影（在我们的例子中是透视投影矩阵），以便将世界坐标映射到裁剪空间坐标。

视图空间 → 投影矩阵 → 裁剪空间

练习

  • 在场景中移动相机。
  • 在视图矩阵中添加一些旋转矩阵以环顾四周。
  • 最后，跟踪鼠标的位置。使用 2 个旋转矩阵，根据用户鼠标在屏幕上的位置，使相机上下看。

另见

帮助改进 MDN

了解如何贡献

此页面最后由MDN 贡献者于修改。

在 GitHub 上查看此页面 • 报告此内容问题
© . Content available under a Creative Commons license.